Single fibre pulled out of an epoxy droplet

Finite elment modelling of fibre-epoxy resin microbond test

Here an axisymmetric 2D model of the microdroplet-fibre-stopper blade was made using ABAQUS/CAE.

Detailed results available here [click]

Results for blade at position 0 [click]

Results for blade at position 2 [click]

Results for blade at position 3 [click]

Results for blade at position 4 [click]

Results when maximum separation was defined as crterion for failure [click]

A Python script was prepared for permitting the automatic building of the FEM.

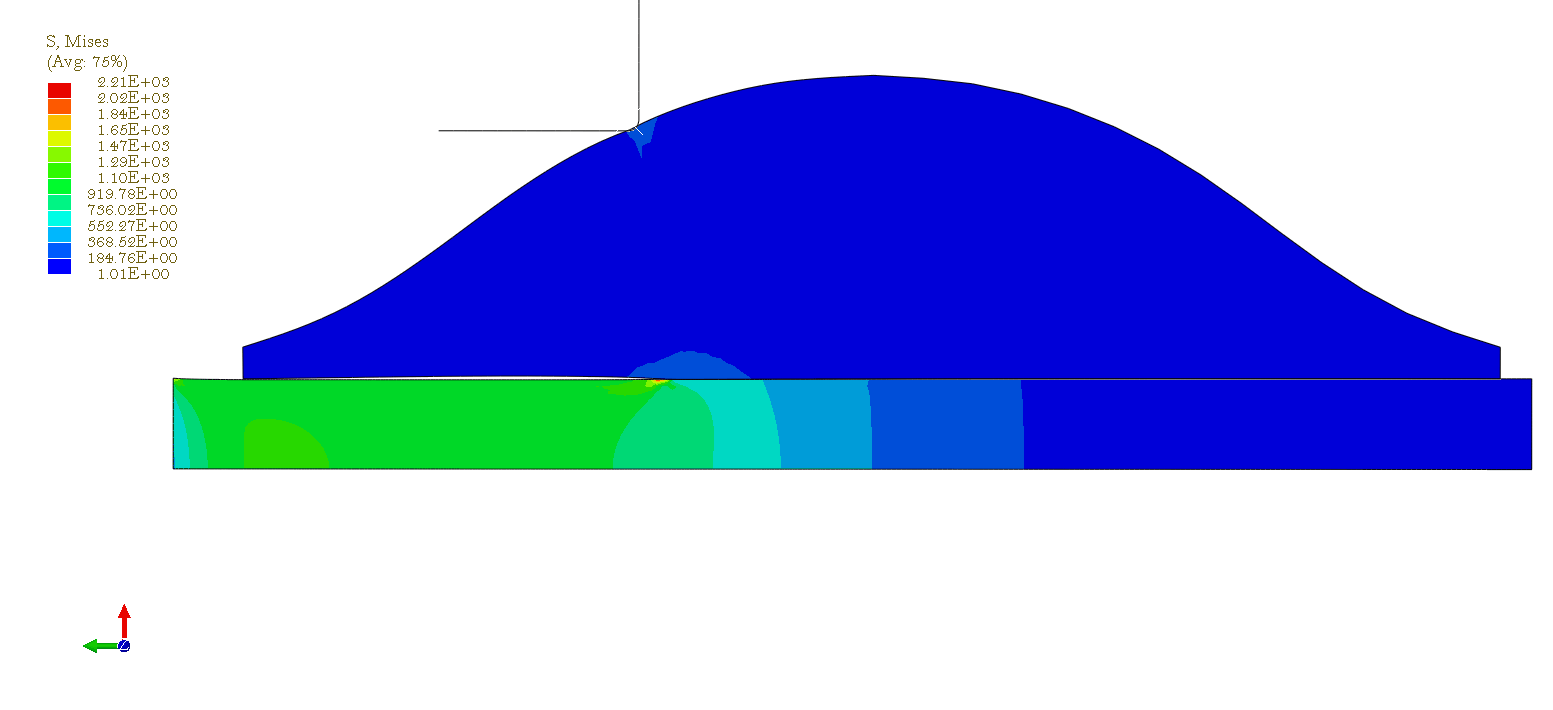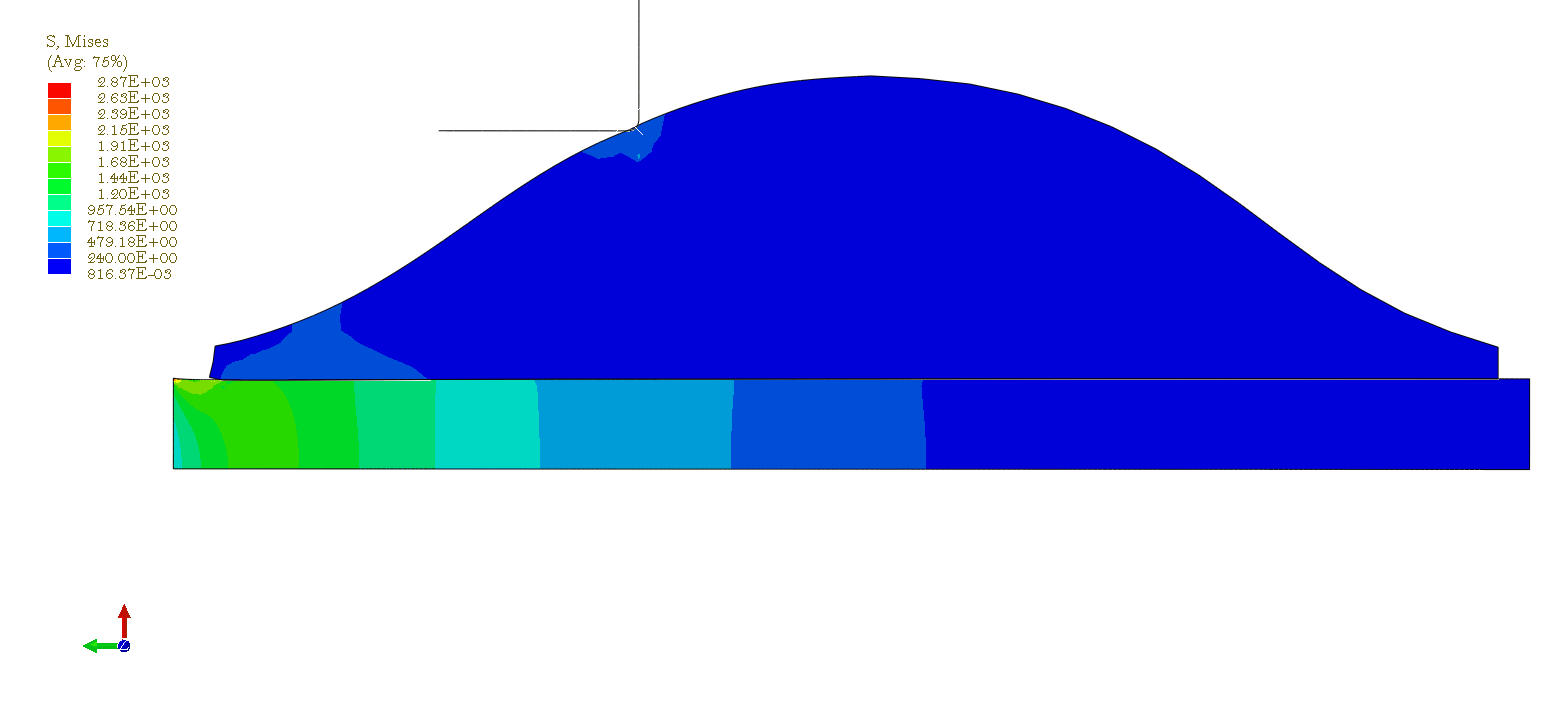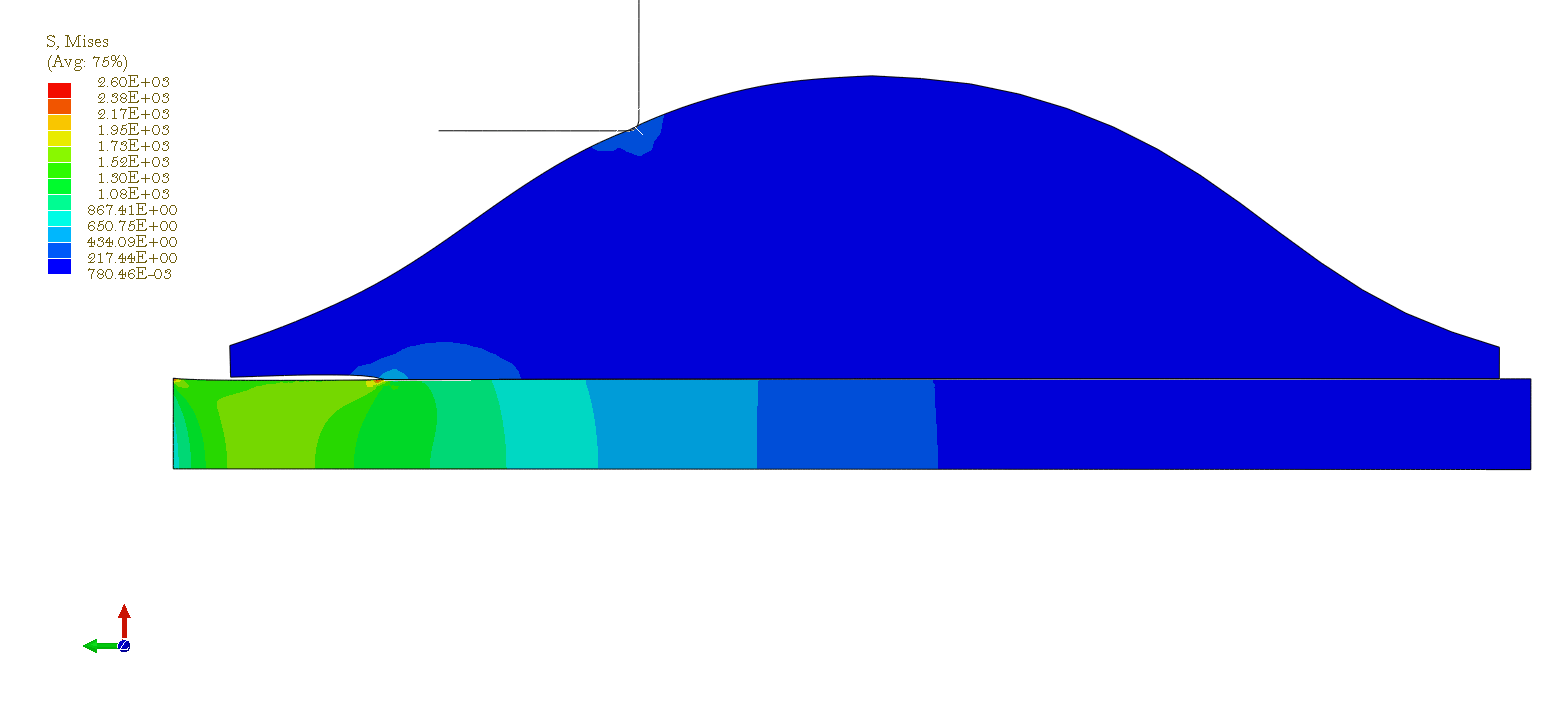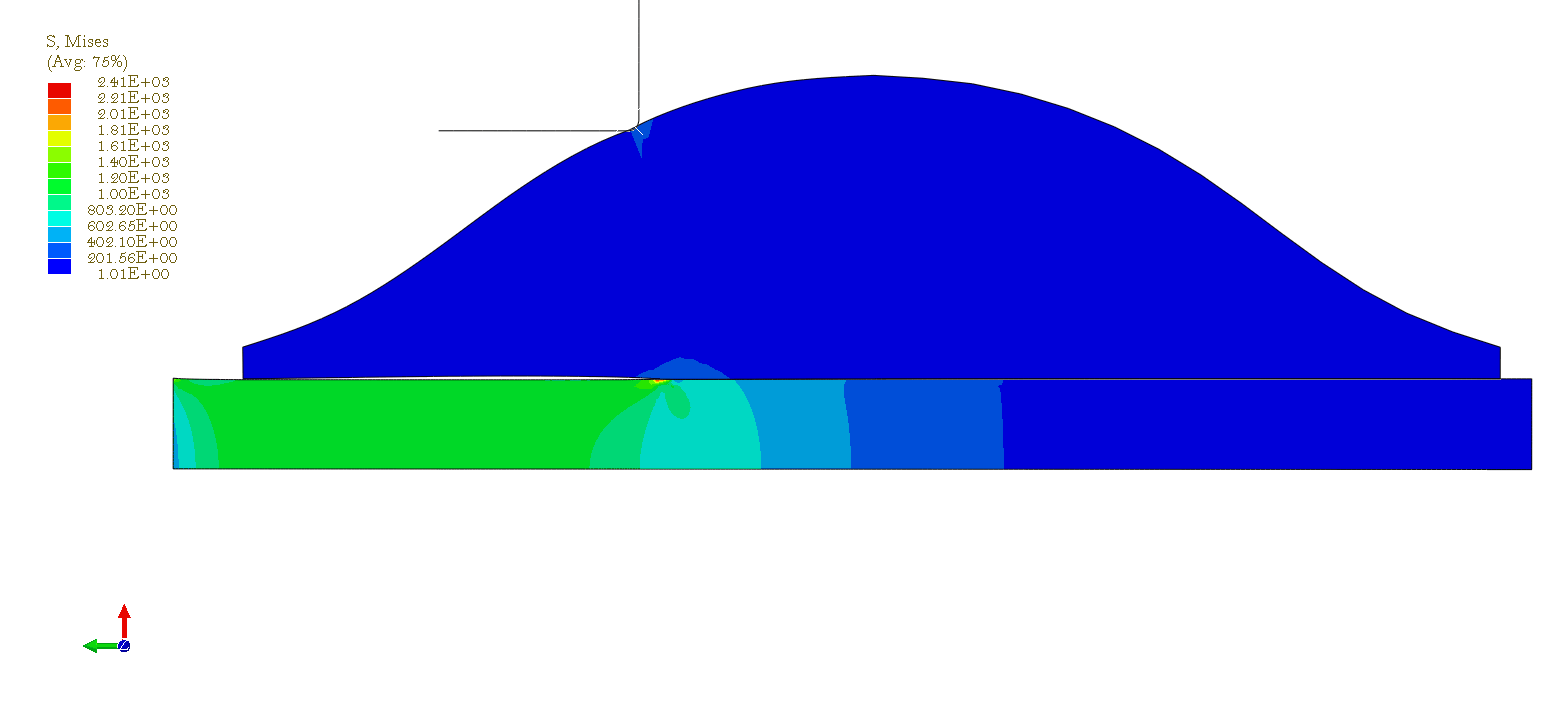
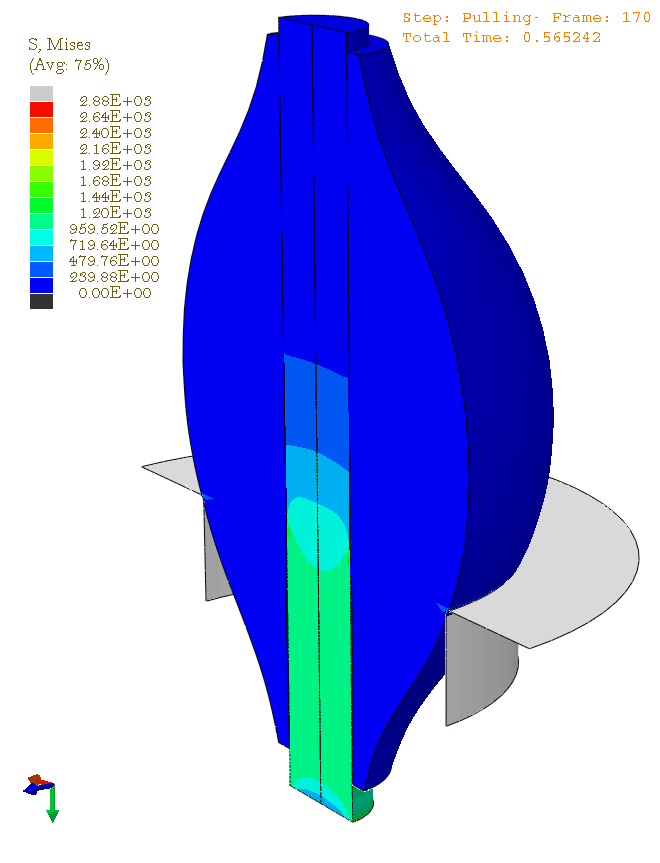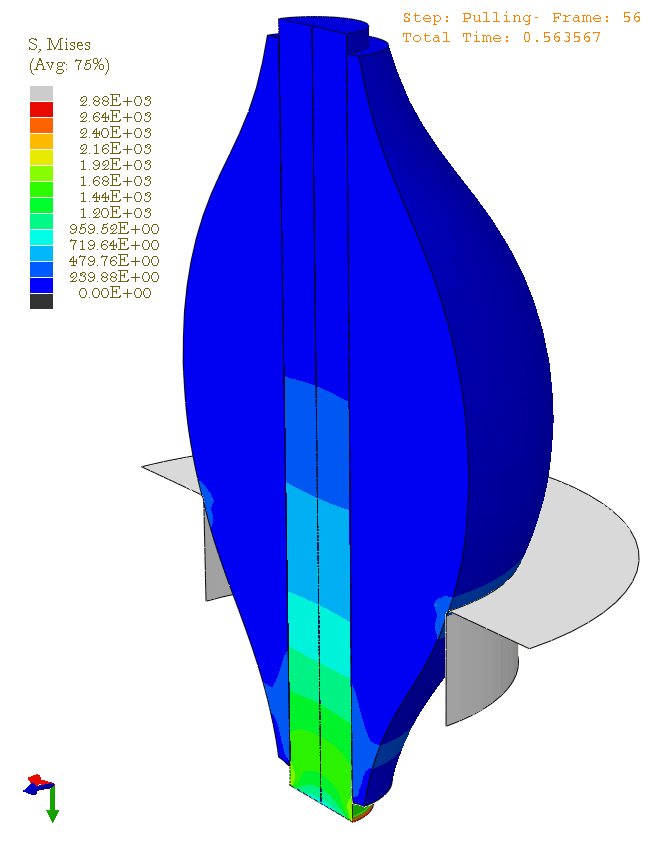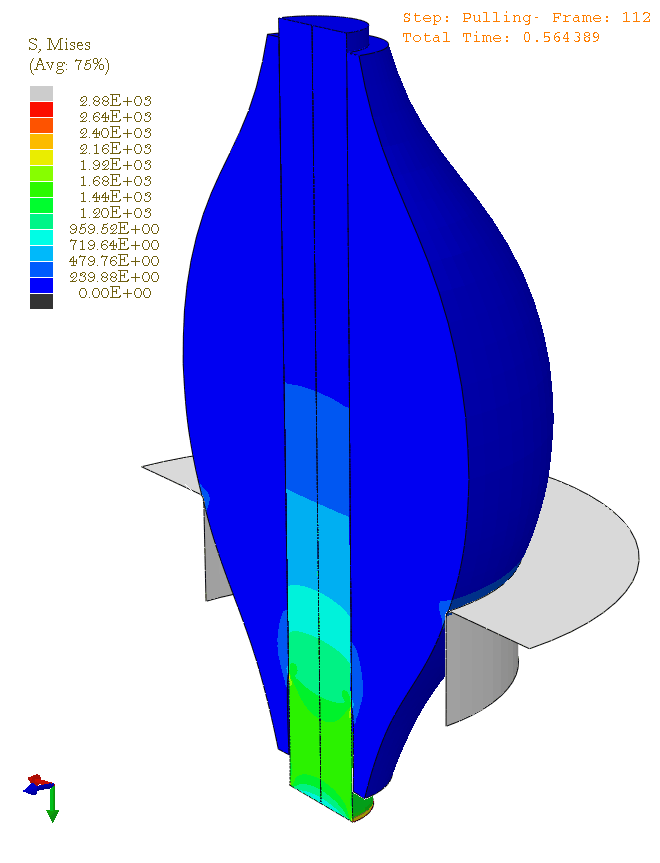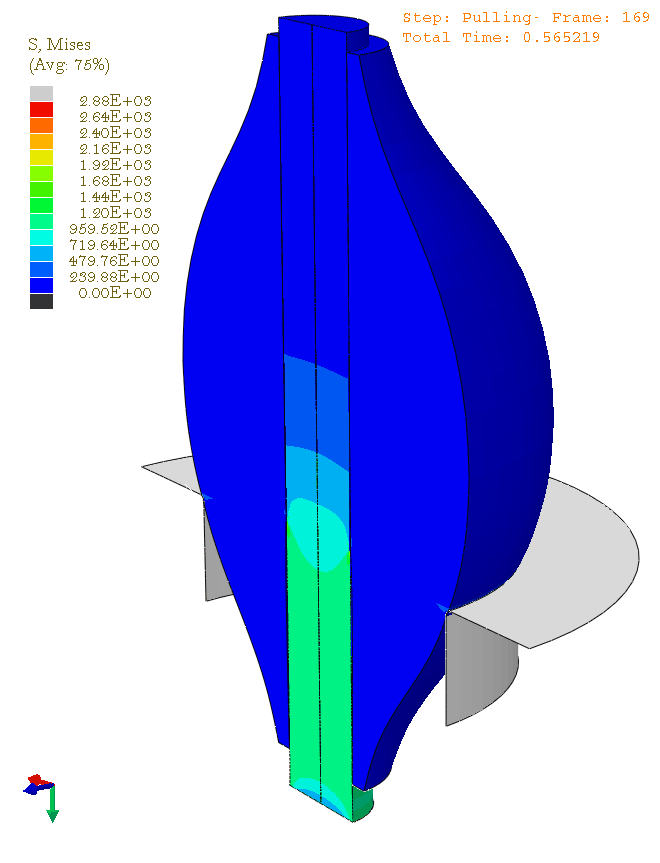
2D rendering of the simulation results - animated frames

3D rendering of the original 2D results - animated frames

Finite Element Modelling

Mesh of the FEM with boundary conditions

Stree levels [MPa] in the model assembly at the maximum load (0.4 N)

Von Mises stree levels [MPa] in the droplet at the maximum load (0.4 N)

Normal stree levels [MPa] in the droplet at the maximum load (0.4 N) - S11

Normal stree levels [MPa] in the droplet at the maximum load (0.4 N) - S22

Normal stree levels [MPa] in the droplet at the maximum load (0.4 N) - S33

Shear stree levels [MPa] in the droplet at the maximum load (0.4 N) - S12

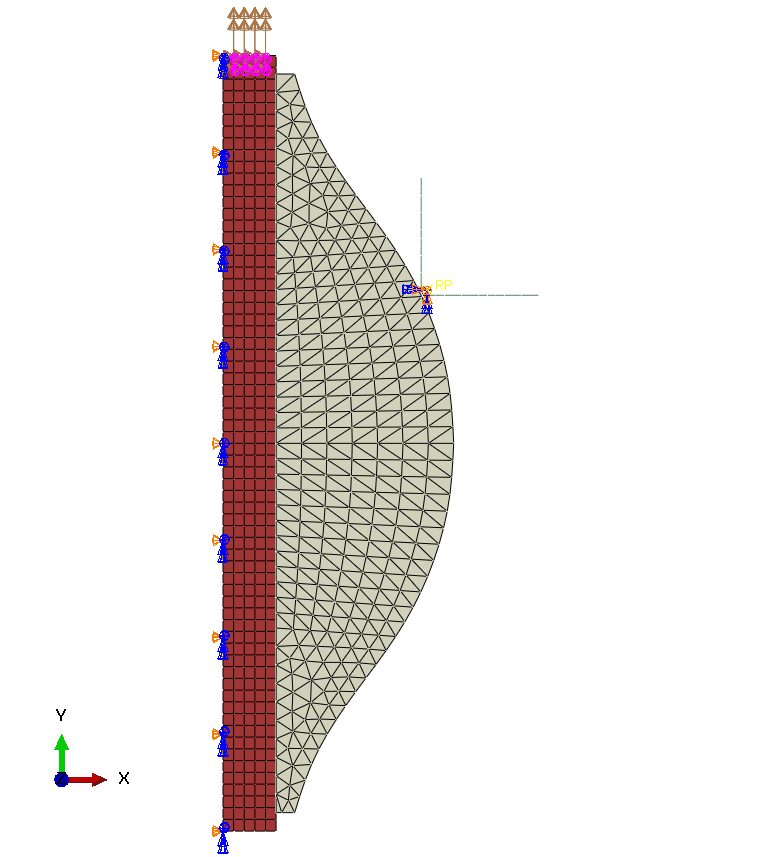
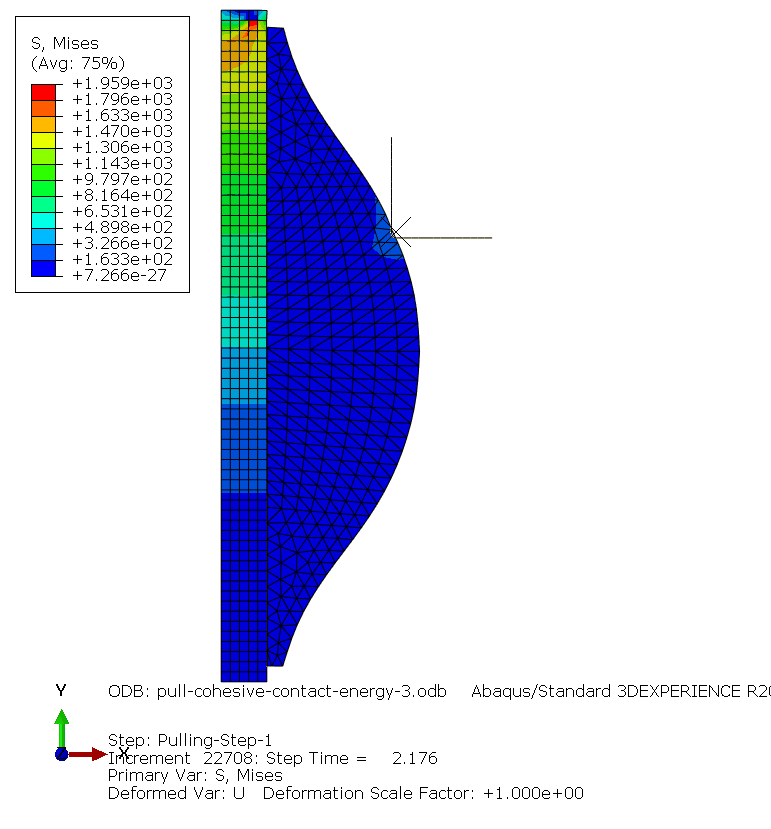
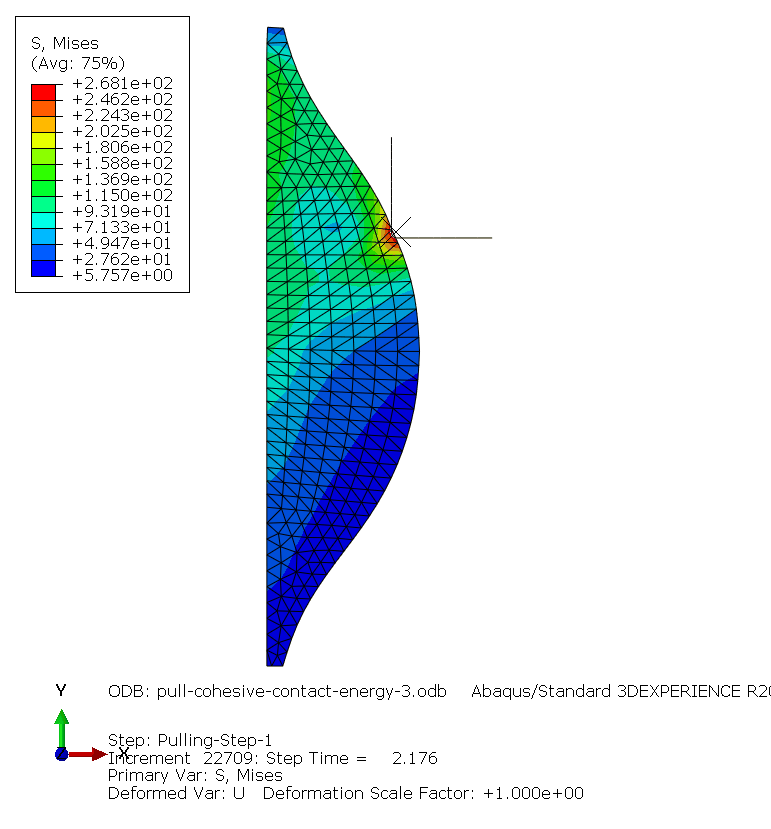
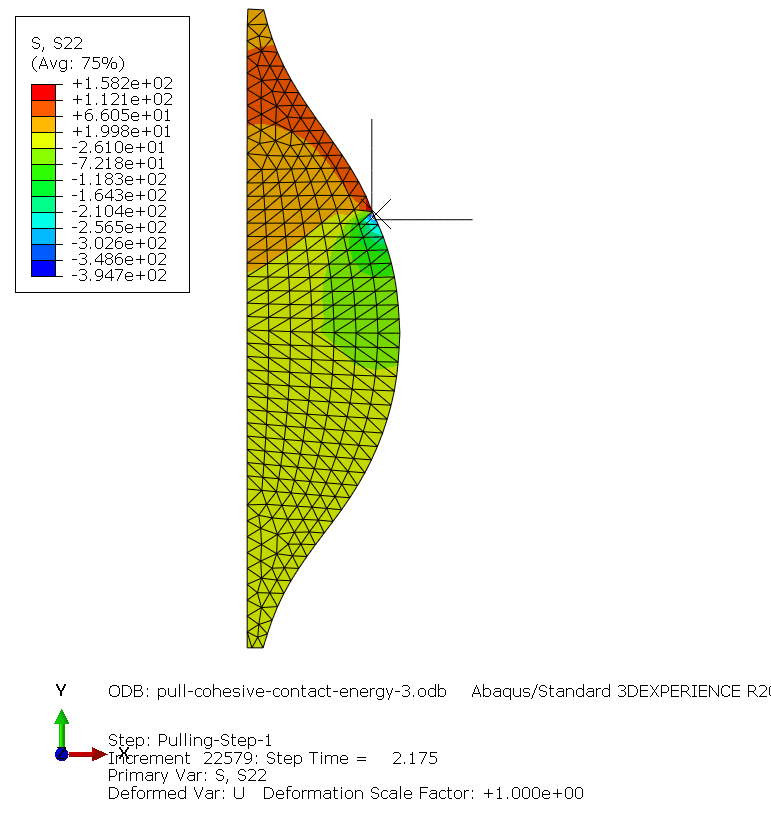
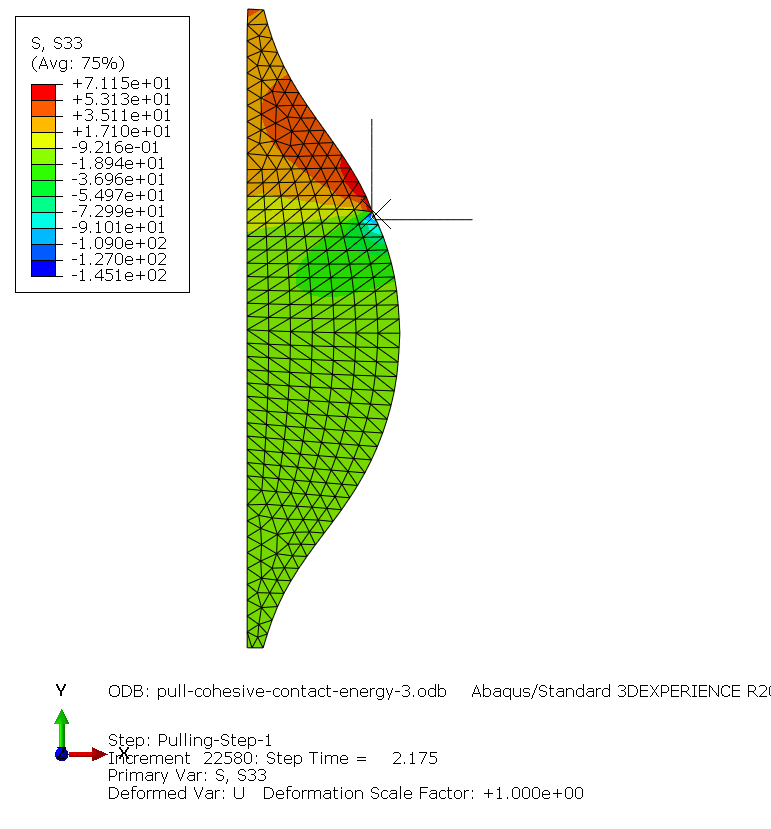
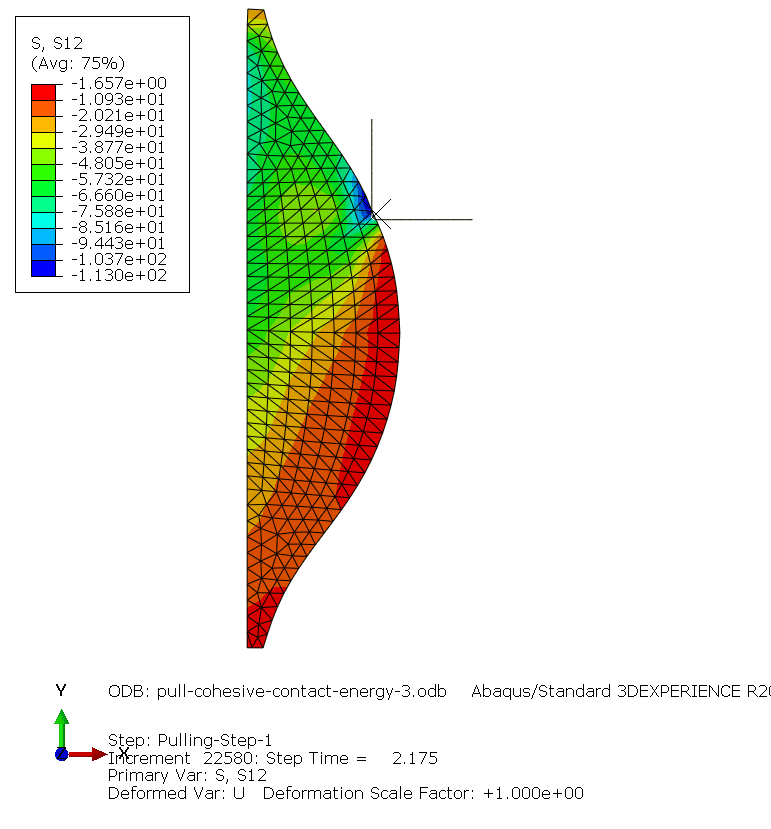
Damage model

Maximum nominal shear stress [Shear-1 Only] for damage initiation was 100 MPa. Normal Only and Shear-2 Only did not affect the results.

Alternatively a shear seperation of 1.2E-07 mm as separation at damage initiation, also gave the same result

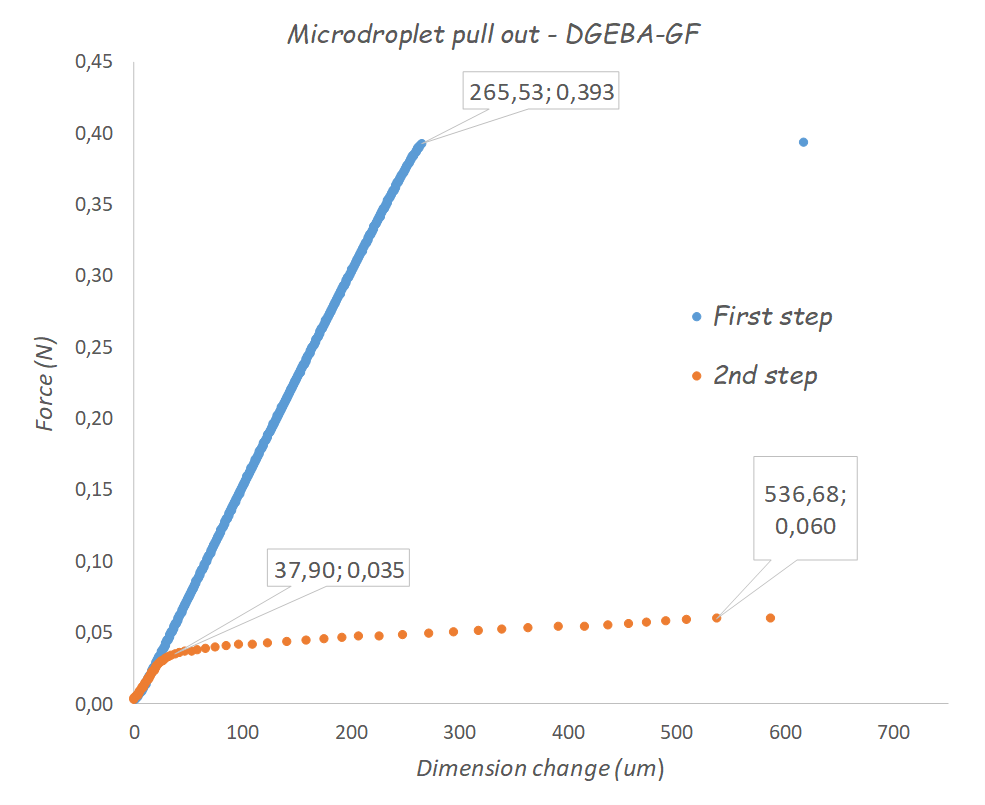
Load v deformation data

Load-displacement results from the 2D simulation -

Experimental data

Microscopic image of the microdroplet on the fibre

Load-displacement results from experiment

Notes:

Comparing the deflection values in the figure above with the droplet dimensions (i.e. 150 micron) shows that the deflection has continued uniformly for more than twice the size of the fibre-droplet interface.

A possible explanation could be that the there is some milimeters of the fibre attached to the fibre-droplet assembly as shown in the first figure above. And the measured large deflection is mostly the elongation of that piece of fibre. This kind of larger than expected deformations have been also reported previously in other works.

Elongation of the fibre

Given the fomula for tensile elongation: $δ L = \frac{P L}{E A}$ $δ L = \frac{P L}{E A}$ , and the values from the fisrt step of the experiment:

Load at the maximum displament, P = 0.393 N,

Length of the fibre, L = 17.64 mm

Fibre diameter, d = 0.0120 mm , or fibre section area: A = 0.0001131 mm²

Maximum recorded displacement, δL = 0.265 mm

would give: E ≅ 230 GPa.

Thus, the Young's modulus of the fibre should not be smaller than 230 GPa. Because lower values would mean that the deformation due to the elongation in the fibre alone will exceed the total displacement of 265 micron.

Counterpoint

The load is transferred from the fiber to the droplet by shear:

By considering the constraint the effective resistant section is the base of the droplet (ring shaped), then I would evaluate the stiffness of the system as compliant to those of the polymer 2,4-2,8 GPa (w is sligthly lower than droplet length 120-130um)

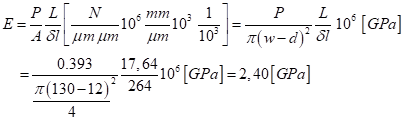
the elastic modulus of E-glass fiber is 70-75 GPa

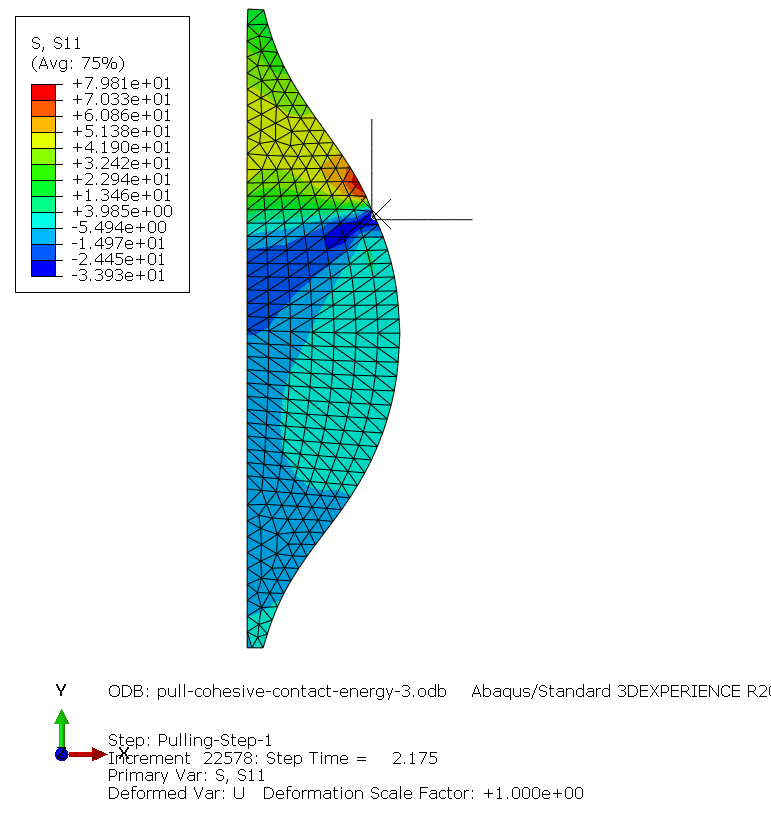
Shear stress in the droplet-fibre bond

Shear stress in the interface: $τ = \frac{F}{π d l}$ $τ = \frac{F}{π d l}$ :

Therefore shear stress at the interface is calculated as: 83.43 [MPa]